أدخل كلمة أو عبارة بأي لغة 👆
اللغة:
ترجمة وتحليل الكلمات عن طريق الذكاء الاصطناعي ChatGPT
في هذه الصفحة يمكنك الحصول على تحليل مفصل لكلمة أو عبارة باستخدام أفضل تقنيات الذكاء الاصطناعي المتوفرة اليوم:
- كيف يتم استخدام الكلمة في اللغة
- تردد الكلمة
- ما إذا كانت الكلمة تستخدم في كثير من الأحيان في اللغة المنطوقة أو المكتوبة
- خيارات الترجمة إلى الروسية أو الإسبانية، على التوالي
- أمثلة على استخدام الكلمة (عدة عبارات مع الترجمة)
- أصل الكلمة
%ما هو (من)٪ 1 - تعريف
Тепловые процессы; Термодинамический процесс; Термодинамические процессы; Обратимые и необратимые процессы
Множественные процессы
рождение большого числа вторичных сильно взаимодействующих частиц (адронов (См. Адроны)) в одном акте столкновения частиц при высокой энергии. М. п. характерны для столкновения адронов, однако в редких случаях они наблюдаются и при столкновениях других частиц, если их энергия достаточна для рождения нескольких адронов (например, при электронных столкновениях на ускорителях со встречными пучками). При столкновениях адронов с энергией выше нескольких Гэв М. п. доминируют над процессами одиночного рождения мезонов и упругого рассеяния частиц. Впервые М. п. наблюдались в космических лучах (См. Космические лучи), однако тщательное их изучение стало возможным после создания ускорителей заряженных частиц высоких энергий. В результате исследований взаимодействия частиц космических лучей с энергией до 106-107 Гэв в лабораторной системе координат, а также частиц от ускорителей с энергией до Множественные процессы 103 Гэв (встречные пучки) выявлены некоторые эмпирические закономерности М. п.
С наибольшей вероятностью в М. п. рождаются самые лёгкие адроны - nи-мезоны (См. Пи-мезоны), составляющие 70-80 \% вторичных частиц. Значительную долю составляют также К-мезоны и Гипероны (Множественные процессы 10-20 \%) и нуклон-антинуклонные пары (порядка нескольких процентов). Многие из этих частиц возникают от распада рождающихся Резонансов.
Вероятность столкновения, сопровождаемого М. п. (эффективное сечение М. п.), при высоких энергиях почти не зависит от энергии сталкивающихся частиц (меняется не более чем на несколько десятков процентов при изменении энергии столкновения в 104 раз). Приблизительное постоянство сечения М. п. привело к модели "чёрных шариков" для описания процессов столкновения адронов. Согласно этой модели, при каждом сближении адронов высокой энергии на расстояния, меньшие радиуса действия ядерных сил, происходит неупругий процесс множественного рождения частиц; упругое рассеяние при этом носит в основном дифракционный характер (дифракция волн де Бройля (См. Волны де Бройля) частиц на "чёрном шарике"). Эта модель сыграла важную роль в развитии теории сильных взаимодействий (в частности, в установлении теоремы Померанчука о равенстве эффективных сечений взаимодействия частиц и античастиц при предельно высоких энергиях). С другой стороны, согласно квантовой теории поля, возможен медленный рост сечения М. п. с увеличением энергии Е, не быстрее, чем ln2Е (теорема Фруассара).
Число частиц, рождающихся в различных актах столкновения адронов определённой энергии, сильно варьирует и в отдельных случаях оказывается очень большим (рис. 1). Среднее число вторичных частиц (средняя множественность) медленно растет с ростом энергии столкновения Е и практически не зависит от типа сталкивающихся адронов (рис. 2). При существующей точности измерений зависимость от энергии одинаково хорошо описывается как логарифмической, так и степенной (типа Ev; v < 1 ) функцией от энергии, что затрудняет выбор между различными теоретическими моделями М. п., предсказывающими разные типы этой зависимости. Средняя множественность много меньше максимально возможного числа вторичных частиц, которое определяется условием, что вся энергия столкновения в системе центра инерции (с. ц. и.) сталкивающихся частиц переходит в массу покоя вторичных частиц. Так, при столкновении протонов с энергией 70 Гэв (от Серпуховского ускорителя) с протонами мишени могло бы рождаться до 70 π-мезонов, в действительности же средняя множественность заряженных частиц при этой энергии составляет 5-6 частиц. Это означает, что на создание массы покоя вторичных частиц идёт только небольшая часть энергии столкновения, т. е. энергия тратится главным образом на сообщение овной части генерированных частиц большой кинетической энергии (большого импульса). В то же время характерной эмпирической закономерностью М. п. является то, что поперечные (к оси соударения) компоненты р⊥ импульсов вторичных частиц, как правило, малы. Среднее значение р⊥; составляет приблизительно 0,3-0,4 Гэв/с и почти постоянно в очень широкой области энергий. Поэтому вторичные частицы вылетают резко направленными и сужающимися по мере роста энергии потоками вдоль направления движения сталкивающихся частиц (в с. ц. и. - вперёд и назад, в лабораторной системе - по направлению движения налетающей частицы).
Изучение М. п. очень существенно для выяснения структуры адронов и построения теории сильных взаимодействий. В этом отношении особое значение имеют закономерности, установленные при изучении специального класса М. п. - т. н. инклюзивных процессов, когда из большого числа М. п., происходящих при столкновениях адронов "а" и "b", отбираются события с рождением определённой частицы "с" независимо от того, какие др. частицы (X) и в каком количестве сопровождают рождение частицы "с". На важность изучения инклюзивных процессов указал в 1967 А. А. Логунов, установивший на основе квантовой теории поля предельные законы возрастания их сечения с ростом энергии (аналогичные теореме Фруассара). При экспериментальном исследовании инклюзивных процессов на Серпуховском ускорителе (1968) и сравнении полученных данных с результатами опытов при более низких энергиях был обнаружен своеобразный закон подобия в микромире - т. н. масштабная инвариантность, или скейлинг (scaling). Масштабная инвариантность состоит в том, что вероятность рождения "инклюзивной" частицы "с" с определённым значением продольного импульса pL, (проекции импульса на направление движения сталкивающихся частиц) является при разных энергиях столкновения универсальной функцией от переменной Х = pL/pмакс, где рмакс - максимально возможное (при данной энергии) значение продольного импульса частицы "с" (рис. 3). Т. о., продольные импульсы вторичных частиц растут пропорционально энергии столкновения. Указания на существование такого рода зависимости получались ранее при изучении космических лучей. Она вытекала из того факта, что энергетический спектр вторичной компоненты космических лучей почти точно повторяет форму энергетического спектра первичной компоненты (Г. Т. Зацепин и др.). Масштабная инвариантность имеет глубокий физический смысл. Объяснение её на основе модельных представлений о составном строении адронов было предложено в 1969 Р. Фейнманом. (В 1963 на возможность такой закономерности указывал американский физик К. Уилсон.)
Экспериментальные данные показывают, что масштабная инвариантность наблюдается при столкновениях не только элементарных частиц, но и атомных ядер при релятивистских энергиях.
Из-за отсутствия полной и последовательной теории сильных взаимодействий для объяснения эмпирических закономерностей, обнаруженных в М. п., используются различные теоретические модели. В статистико-гидродинамических моделях [развитых в работах В. Гейзенберга, Э. Ферми, Л. Д. Ландау (1949-53) и др.] предполагается, что для сильно взаимодействующих частиц в течение короткого времени столкновения успевает установиться статистическое равновесие между образовавшимися в результате соударения частицами. Это позволяет рассчитать многие характеристики М. п., в частности среднюю множественность, которая должна расти с энергией по степенному закону Еν с показателем степени ν < 1 (в теории Ферми - Ландау ν = 1/4). В другом классе моделей (итальянские физики Д. Амати, С. Фубини, А. Стангеллини и др., советские физики Е. Л. Фейнберг, Д. С. Чернавский и др.) считается, что рождение вторичных частиц происходит в "периферических" или "мультипериферических" взаимодействиях адронов, возникающих в результате обмена между ними виртуальным π-мезоном или другой частицей. С конца 60-х гг. для теоретического анализа М. п. широко используется представление о том, что сильное взаимодействие при высоких энергиях осуществляется путём обмена особым состоянием - "реджеоном", являющимся как бы струей частиц с монотонно меняющимся от частицы к частице импульсом (см. Сильные взаимодействия). Эти представления (развитые, в частности, советскими физиками В. Н. Грибовым, К. А. Тер-Мартиросяном и др.) позволяют количественно объяснить многие закономерности М. п. Согласно "мультипериферическим" моделям и модели "реджеонов", средняя множественность должна расти пропорционально логарифму энергии столкновения.
Лит.: Мурзин В. С., Capычева Л. И., Множественные процессы при больших энергиях, М., 1974 (в печати); Беленький С. З., Ландау Л. Д., Гидродинамическая теория множественного образования частиц, "Успехи физических наук", 1955, т. 56, в. 3, с. 309; Фейнберг Е. Л., Множественная генерация адронов и статистическая теория, там же, 1971, т. 104, в. 4, с. 539; Feynman R., Very high-energy collisions of hadrons, "Physical Review Letters", 1969, v. 23, p. 1415; Ежела В. В. [и др.]. Инклюзивные процессы при высоких энергиях, "Теоретическая и математическая физика", 1973, т. 15, № 2; Тер-Мартиросян К. А., Процессы образования частиц при высокой энергии, в кн.: Материалы 6-й зимней школы по теории ядра и физике высоких энергий, ч. 2, Л., 1971, с. 334; Розенталь И. Л., Множественные процессы при больших энергиях, "Природа", 1973, № 12.
С. С. Герштейн.
Рис. 2. Среднее число вторичных заряженных частиц nс как функция кинетической энергии Q сталкивающихся частиц в системе их центра инерции. Разными значками обозначены результаты, относящиеся к рассеянию π±-, К±-мезонов и протонов на нуклонах.
Рис. 3. График, иллюстрирующий масштабную инвариантность в инклюзивном процессе р+р→π-+Х (р - протон, π- - отрицательный π-мезон, Х - совокупность остальных адронов, родившихся в реакции). Зависимость величины (2/π)xdσ/dx, пропорциональной дифференциальному сечению рождения π--мезона dσ/dx, от х=рL/pмaкс; экспериментальные данные при различных энергиях столкновения с точностью до ошибок измерения укладываются в универсальную зависимость от х. Разными значками помечены данные, относящиеся к различным энергиям (импульсам) столкновения в лабораторной системе; точки при 1500, 1100, 500, 270 Гэв/с получены в опытах на ускорителе со встречными пучками в ЦЕРНе, при 70 Гэв/с - в советско-французском эксперименте в Серпухове.
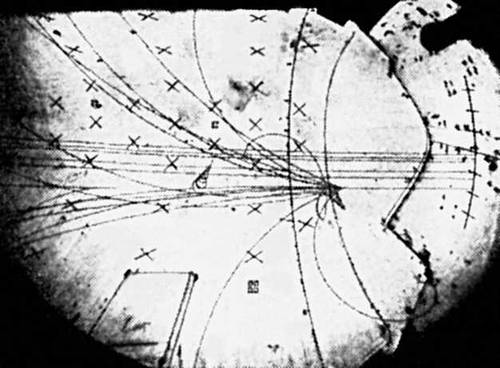
Рис. 1. Фотография множественного рождения заряженных частиц, полученная в жидководородной пузырьковой камере "Мирабель", помещенной в пучок π-мезонов с энергией 50 Гэв на Серпуховском ускорителе.
Энергетические процессы в клетке
Энергетические процессы в клетке — процессы обмена веществ, обеспечивающие снабжение клеток энергией для выполнения актов жизнедеятельности. В основном они относятся к процессам катаболизма, так как среди них важное значение имеет расщепление богатых энергией (питательных) веществ.
Фотографические процессы
СТАТЬЯ-СПИСОК В ПРОЕКТЕ ВИКИМЕДИА
Фотографический процесс; Типографические процессы
Фотографические процессы — совокупность технологий, позволяющая получить фотографическое изображение на фотоматериалах.
ويكيبيديا
Тепловой процесс
Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы. Если разница между начальным и конечным состояниями системы бесконечно мала, то такой процесс называют элементарным (инфинитезимальным).
Система, в которой идёт тепловой процесс, называется рабочим телом.
Тепловые процессы можно разделить на равновесные и неравновесные. Равновесным называется процесс, при котором все состояния, через которые проходит система, являются равновесными состояниями. Такой процесс приближённо реализуется в тех случаях, когда изменения происходят достаточно медленно, т. е. процесс является квазистатическим.
Тепловые процессы можно разделить на обратимые и необратимые. Обратимым называется процесс, который можно провести в противоположном направлении через все те же самые промежуточные состояния.
Процессы принято классифицировать по тем термодинамическим величинам, которые остаются неизменными в ходе процесса. Можно выделить несколько простых, но широко распространённых на практике, тепловых процессов:
- Адиабатный процесс ()— без теплообмена с окружающей средой;
- Изохорный процесс () — происходящий при постоянном объёме;
- Изобарный процесс () — происходящий при постоянном давлении ;
- Изотермический процесс () — происходящий при постоянной температуре;
- Изоэнтропийный процесс ()— происходящий при постоянной энтропии;
- Изоэнтальпийный процесс ()— происходящий при постоянной энтальпии;
- Политропный процесс ()— происходящий при постоянной теплоёмкости.
Иногда в течение всего процесса неизменными оказываются не одна, а несколько термодинамических величин. Так, например, испарение и конденсация в системе жидкость — пар, когда одновременно постоянны и давление и температура, есть процессы изобарно-изотермические.
В технике важны круговые процессы (циклы), то есть повторяющиеся процессы, например, цикл Карно, цикл Ренкина.
Теория тепловых процессов применяется для проектирования двигателей, холодильных установок, в химической промышленности, в метеорологии.
