Ingrese una palabra o frase en cualquier idioma 👆
Idioma:
Traducción y análisis de palabras por inteligencia artificial ChatGPT
En esta página puede obtener un análisis detallado de una palabra o frase, producido utilizando la mejor tecnología de inteligencia artificial hasta la fecha:
- cómo se usa la palabra
- frecuencia de uso
- se utiliza con más frecuencia en el habla oral o escrita
- opciones de traducción
- ejemplos de uso (varias frases con traducción)
- etimología
Qué (quién) es Брэгга - Вульфа условие - definición
Дифракция Брэгга; Брэгговская дифракция; Условие Вульфа-Брэгга; Формула Брэгга — Вульфа; Закон Брэгга; Решетка Брэгга; Дифракция рентгеновских лучей; Дифракция Брегга; Брэгга — Вульфа условие; Брэгга – Вульфа условие; Условие Вульфа — Брэгга
Условие Брэгга — Вульфа
Условие Брэгга — Вульфа определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в 1913 независимо У.
ДИФРАКЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
рассеяние рентгеновских лучей кристаллическими объектами, при котором в определенных направлениях появляются дифрагированные пучки - результат интерференции вторичного рентгеновского излучения, возникающего при взаимодействии первичного излучения с электронными оболочками атомов. Направление и интенсивность дифрагированных пучков связаны с атомной структурой объекта (см. Брэгга - Вульфа условие, Рентгеновский структурный анализ).
Дифракция рентгеновских лучей
рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения. Наряду с рассеянием без изменения длины волны наблюдается рассеяние с изменением длины волны - так называемое комптоновское рассеяние (см. Комптона эффект). Явление Д. р. л., доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912.
Кристалл является естественной трёхмерной дифракционной решёткой (См. Дифракционная решётка) для рентгеновских лучей, т.к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (Дифракция рентгеновских лучей1Å=10-8 см). Д. р. л. на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллической решётки (см. Брэгга - Вульфа условие). Направление дифракционных максимумов удовлетворяет одновременно трём условиям:
a (cos α - cos α0) = Нλ,
b (cos β - cos β0) = Kλ,
с (cos γ - cos γ0) = Lλ.
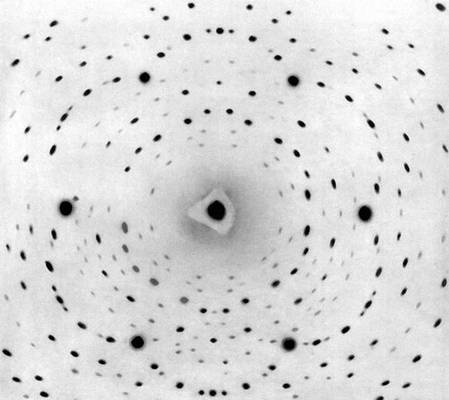
Здесь а, b, с - периоды кристаллической решётки (См. Кристаллическая решётка) по трём её осям; α0, β0, γ0 - углы, образуемые падающим, а α, β, γ - рассеянным лучами с осями кристалла; λ - длина волны рентгеновских лучей, Н, К, L - целые числа. Эти уравнения называются уравнениями Лауэ. Дифракционную картину получают либо от неподвижного кристалла с помощью рентгеновского излучения со сплошным спектром (так называемая Лауэграмма; рис. 1), либо от вращающегося или колеблющегося кристалла (углы α0, β0 меняются, а γ0 остаётся постоянным), освещаемого монохроматическим рентгеновским излучением (λ - постоянно), либо от поликристалла, освещаемого монохроматическим излучением. В последнем случае, благодаря тому что отдельные кристаллы в образце ориентированы произвольно, меняются углы α0, β0, γ0.
Интенсивность дифрагированного луча зависит в первую очередь от так называемого структурного фактора, который определяется атомными факторами (См. Атомный фактор) атомов кристалла, их расположением внутри элементарной ячейки кристалла, а также характером тепловых колебаний атомов. Структурный фактор зависит от симметрии расположения атомов в элементарной ячейке. Интенсивность дифрагированного луча зависит также от размеров и формы объекта, от совершенства кристалла и прочего.
Д. р. л. от поликристаллических тел приводит к возникновению резко выраженных конусов вторичных лучей. Осью конуса является первичный луч, а угол раствора конуса равен 4ϑ (ϑ - угол между отражающей плоскостью и падающим лучом). Каждый конус соответствует определённому семейству кристаллических плоскостей. В создании конуса участвуют все кристаллики, семейство плоскостей которых расположено под углом ϑ к падающему лучу. Если кристаллики малы и их приходится очень большое количество на единицу объёма, то конус лучей будет сплошным. В случае текстуры, т. е. наличия предпочтительной ориентировки кристалликов, дифракционная картина (Рентгенограмма) будет состоять из неравномерно зачернённых колец (см. также Дебая - Шеррера метод).
Метод Д. р. л. на кристаллах дал возможность определять длину волны рентгеновских лучей, если известна структура кристаллической решётки, благодаря чему возникла Рентгеновская спектроскопия, сыгравшая важную роль при установлении строения атома. Наблюдения Д. р. л. известной длины волны на кристалле неизвестной структуры позволяют установить характер этой структуры (расположение ионов, атомов и молекул, составляющих кристалл), что послужило основой рентгеновского структурного анализа (См. Рентгеновский структурный анализ).
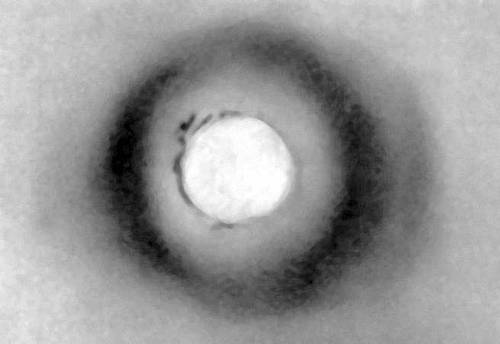
Д. р. л. наблюдается также при рассеянии их аморфными твёрдыми телами, жидкостями и газами. В этом случае на кривой зависимости интенсивности от угла рассеяния вокруг центрального пятна появляются широкие кольца типа гало (рис. 2). Положение этих колец (угол ϑ) определяется средним расстоянием между молекулами или расстояниями между атомами в молекуле. Из зависимости интенсивности от угла рассеяния можно определить распределение плотности вещества.
Д. р. л. можно наблюдать также на обычной оптической дифракционной решётке при скользящем падении (меньше угла полного отражения) рентгеновских лучей на решётку. С помощью этого метода можно непосредственно и с большой точностью измерять длины волн рентгеновских лучей.
Лит.: Ландсберг Г. С., Оптика, 4 изд., М., 1957 (Общий курс физики, т. 3); Боровский И. Б., Физические основы рентгеноспектральных исследований, М., 1956.
В. И. Иверонова.
Рис. 1. Лауэграмма берилла.
Рис. 2. Рентгенограмма воды.
Wikipedia
Условие Брэгга — Вульфа
Условие Брэгга — Вульфа определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в 1913 независимо У. Л. Брэггом и Г. В. Вульфом. Имеет вид:
где d — межплоскостное расстояние, θ — угол скольжения (брэгговский угол), n — порядок дифракционного максимума, λ — длина волны.
Брэгговская дифракция может наблюдаться не только для электромагнитных волн, но и для волн материи (волновых функций). В частности, экспериментально это было впервые продемонстрировано для нейтронов в 1936 году, а позднее также для отдельных атомов, конденсата Бозе — Эйнштейна, электронов, двухатомных и многоатомных молекул.
