Введите слово или словосочетание на любом языке 👆
Язык:
Перевод и анализ слов искусственным интеллектом ChatGPT
На этой странице Вы можете получить подробный анализ слова или словосочетания, произведенный с помощью лучшей на сегодняшний день технологии искусственного интеллекта:
- как употребляется слово
- частота употребления
- используется оно чаще в устной или письменной речи
- варианты перевода слова
- примеры употребления (несколько фраз с переводом)
- этимология
Что (кто) такое мера - определение
СТРАНИЦА ЗНАЧЕНИЙ В ПРОЕКТЕ ВИКИМЕДИА
Мера вероятности; Мера (река)
Найдено результатов: 323
МЕРА
в России емкость для измерения жидких и сыпучих тел. Обычно равна четверику (26,24 л).
---
1) философская категория, выражающая диалектическое единство качества и количества объекта; указывает предел, за которым изменение количества влечет за собой изменение качества объекта и наоборот.2) Мера как соразмерность лежит в основе ритма, гармонии, мелодии в музыке, ансамбля в архитектуре и т. п.3) Мера в метрологии - см. Меры.
---
(Mera) Хуан Леон (1832-94) , эквадорский политический деятель, писатель-романтик. Председатель сената и министр в правительстве Г. Гарсии Морено. Стихи (сборник "Туземные мелодии" 1858, текст Национального гимна), поэма "Дева солнца" (1861). Первый эквадорский роман - "Куманда" (1879; из колониальной эпохи), проникнутый духом католицизма; рассказы в духе костумбризма.
---
1) философская категория, выражающая диалектическое единство качества и количества объекта; указывает предел, за которым изменение количества влечет за собой изменение качества объекта и наоборот.2) Мера как соразмерность лежит в основе ритма, гармонии, мелодии в музыке, ансамбля в архитектуре и т. п.3) Мера в метрологии - см. Меры.
---
(Mera) Хуан Леон (1832-94) , эквадорский политический деятель, писатель-романтик. Председатель сената и министр в правительстве Г. Гарсии Морено. Стихи (сборник "Туземные мелодии" 1858, текст Национального гимна), поэма "Дева солнца" (1861). Первый эквадорский роман - "Куманда" (1879; из колониальной эпохи), проникнутый духом католицизма; рассказы в духе костумбризма.
мера
1. Единица измерения протяжения или емкости. Мера длины. Мера веса. Меры сыпучих тел. Кубические меры.
2. Предел, граница, размер. "Чудится, будто... голубая зеркальная дорога без меры в ширину, без конца в длину реет и вьется по зеленому миру." Гоголь (о Днепре). Чувство меры. Соблюдать меру. Знать меру. "Душа меру знает." (посл.).
3. Мероприятие, способ действия. Крайняя мера. Принять или (·устар.) взять меры. Решительные меры. Меры предосторожности. *****
5. Стихотворный размер (лит. ·устар. ).
6. Сосуд для измерения сыпучих тел, четверик (·устар. ·прост. ). Мера овса.
• Без меры - безмерно. Сверх меры или чрез (и ·прост. через) меру - слишком, более надлежащего, чрезмерно. В меру - умеренно, достаточно, сколько нужно. По мере чего (сил, возможности и т.п.) - соответственно, смотря по чему. По мере того, как, в знач. союза - в то время, как; в соответствии с тем, как. По меньшей мере - самое меньшее, самое крайнее, в крайнем случае. Это будет стоить по меньшей мере сто рублей. По крайней мере - см. крайний
. В полной мере - вполне. В той мере, как - постольку, поскольку. Ни в какой мере (·канц.) - никак, никаким образом.
. В полной мере - вполне. В той мере, как - постольку, поскольку. Ни в какой мере (·канц.) - никак, никаким образом.
Мера
I
Ме́ра (Mera)
Хуан Леон (28.6.1832, Амбато, - 13.12.1894, там же), экуадорский писатель и литературный критик. Один из идейных вождей экуадорского консерватизма, председатель сената и министр в годы клерикально-реакционной диктатуры Гарсиа Морено (1869-75). Автор национального гимна. В поэме "Дева солнца" (1861), сборниках стихов "Туземные мелодии" (1858), "Масорра" (1875) М. использовал мотивы индейского фольклора. Роман "Куманда" (1879), написанный в духе европейского романтизма, в идиллических тонах повествует о прошлом индейских племён. Книга М. "Историко-критический обзор экуадорской поэзии" (1868) содержит идею национально-самобытного развития литературы. Автор повестей и очерков нравоописательного характера (см. Костумбризм).
Соч.: Obras, Barcelona, 1887; Novelas cortas, Ambato, 1952.
Лит.: Мамонтов С. П., Литература Эквадора, в сборнике Эквадор, М., 1963; Guevara Dario С., Juan León Mera о el hombre de cimas, Quito, 1944; Arias A., Panorama de la literatura ecuatoriana, Quito, 1961.
С. П. Мамонтов.
II
Ме́ра
в метрологии, см. в ст. Меры.
III
Ме́ра
философская категория, выражающая диалектическое единство качественных и количественных характеристик объекта. Качество любого объекта органически связано с определённым Количеством (свойств, сторон, признаков, размеров, числа компонентов данной системы и т.п.). В рамках данной М. количественной характеристики могут меняться за счёт изменения числа, размеров, порядка связи элементов, скорости движения, степени развития и т.п. М. указывает предел, за которым изменение количества влечёт за собой изменение качества объекта и наоборот. Следовательно, М. - это своего рода зона, в пределах которой данное качество может модифицироваться, сохраняя при этом свои существенные характеристики. М. выступает и как соразмерность; например, грация - как соразмерность, гармония в движении тела. Соблюдение М. лежит в основе ритма, гармонии, мелодии в музыке, ансамбля в архитектуре и т.п. М. употребляется также при измерении (См. Измерение) как определённая единица, с которой соотносят, сравнивают измеряемый объект.
Категория М. имеет существенное теоретическое и практическое значение: нахождение М. в любой форме деятельности служит предпосылкой её успеха. Нельзя познать предмет, не выявив его качественных и количественных характеристик в их единстве.
IV
Ме́ра
река в Костромской и Ивановской области РСФСР, левый приток Волги. Длина 152 км, площадь бассейна 2380 км2. Впадает в Горьковское водохранилище против г. Кинешма. Питание смешанное, с преобладанием снегового. Средний расход в 51 км от устья 6,5 м3/сек. Замерзает в ноябре, вскрывается в апреле.
мера
ж.
1) Единица измерения.
2) а) Старинная русская единица емкости для сыпучих тел, равная приблизительно одному пуду зерна.
б) Сосуд для измерения сыпучих тел, вмещающий такое количество зерна.
3) а) То, чем измеряют что-л.; мерило.
б) перен. То, что служит основанием для оценки, измерения чего-л. или сравнения с чем-л.
4) а) Величина, размер, степень охвата какого-л. явления.
б) Последняя, крайняя степень, предел чего-л.
1) Единица измерения.
2) а) Старинная русская единица емкости для сыпучих тел, равная приблизительно одному пуду зерна.
б) Сосуд для измерения сыпучих тел, вмещающий такое количество зерна.
3) а) То, чем измеряют что-л.; мерило.
б) перен. То, что служит основанием для оценки, измерения чего-л. или сравнения с чем-л.
4) а) Величина, размер, степень охвата какого-л. явления.
б) Последняя, крайняя степень, предел чего-л.
МЕРА
1. средство для осуществления чего-нибудь, мероприятие.
Меры предосторожности. Решительные меры. Принять нужные меры.
2. единица измерения.
Квадратные меры. М. длины. М. веса.
3. граница, предел проявления чего-нибудь.
Знать меру. Чувство меры. Без меры(очень). Сверх меры (слишком). В меру (как раз). В какой мере (насколько).
4. старая русская единица емкости сыпучих тел, а также сосуд для измерения их.
М. овса.
Мера множества
АДДИТИВНАЯ ЧИСЛЕННОЗНАЧНАЯ ФУНКЦИЯ ОТ МНОЖЕСТВА
Носитель меры; Пространство с мерой; Конечно-аддитивная мера; Σ-аддитивность; Теория меры; Счётно-аддитивная мера; Мера (математика); Финитная мера; Меры теория
математическое понятие, обобщающее понятия длины отрезка, площади плоской фигуры и объёма тела на множества более общей природы. В качестве примера можно привести определение меры Лебега (введённой А. Лебегом в 1902) для ограниченных множеств, лежащих на плоскости. При определении меры Лебега, так же как и при определении площади плоских фигур в геометрии, исходят из сравнения части плоскости, занимаемой множеством, с выбранной единицей измерения. При этом и способ сравнения напоминает обычный процесс измерения площади. Меру Лебега m (Δ) любого квадрата Δ полагают равной его площади. Затем рассматриваемое множество А покрывают конечным или бесконечным числом квадратов Δ1, Δ2,..., Δn,...; нижнюю грань чисел
взятую по всевозможным покрытиям множества А, называют верхней (внешней) мерой m*(А) множества А. Нижняя (внутренняя) мера m* (А) множества А определяется как разность
где Δ - какой-либо квадрат, содержащий множество А, и  - множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
- множество всех точек этого квадрата, не содержащихся в А. Множества, для которых верхняя мера равна нижней, называют измеримыми по Лебегу, а общее значение m (А) верхней и нижней мер - мерой Лебега множества А. Геометрические фигуры, имеющие площадь в элементарном смысле (см. Квадрируемая область), измеримы, и их мера Лебега совпадает с их площадью. Однако существуют и неквадрируемые измеримые множества. Аналогично можно определить меру Лебега на прямой. При этом верхнюю меру определяют, рассматривая покрытия множества интервалами.
Основные свойства меры Лебега: 1) мера любого множества неотрицательна: m (A)Δ ́≥ ́0; 2) мера суммы
конечной или счётной системы попарно непересекающихся множеств A1, A2..., An... равна сумме их мер:
3) при перемещении множества как твёрдого тела его мера не меняется.
Своеобразие понятия "М. м." можно пояснить следующим примером: множество А рациональных точек интервала (0, 1) и множество В иррациональных точек того же интервала сходны в том смысле, что каждое из них плотно на интервале (0, 1), т. е., что между любыми двумя точками указанного интервала найдутся как точки множества А, так и точки множества В; в то же время они резко различаются по мере: m (А) = 0, а m (В) = 1.
Для более узких классов множеств мера, совпадающая с лебеговской, была ранее определена М. Э. К. Жорданом (1893) и Э. Борелем (См. Борель) (1898). О других вопросах, связанных с мерой Лебега, см. Интеграл.
Развитие ряда отделов современной математики привело к дальнейшим обобщениям - созданию т. н. абстрактной теории меры. При этом М. м. определяют аксиоматически. Пусть U - произвольное множество и 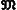 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в  , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в  , сумма А которых входит в
, сумма А которых входит в  , имеет место равенство
, имеет место равенство
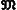 - некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в
- некоторое семейство его подмножеств. Неотрицательную функцию μ(A), определённую для всех А, входящих в  , называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в
, называют мерой, если она вполне аддитивна [т. е., если для любой последовательности непересекающихся множеств A1, A2,..., An,..., входящих в  , сумма А которых входит в
, сумма А которых входит в  , имеет место равенство
, имеет место равенство и если, кроме того, система  удовлетворяет определённым дополнительным условиям. Множества, входящие в
удовлетворяет определённым дополнительным условиям. Множества, входящие в  , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
, называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
 удовлетворяет определённым дополнительным условиям. Множества, входящие в
удовлетворяет определённым дополнительным условиям. Множества, входящие в  , называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования.
, называют измеримыми (по отношению к мере μ). После того как определена мера μ, вводят понятие измеримых (по отношению к μ) функций и операцию интегрирования. Многие основные утверждения из теории меры Лебега, теории измеримых функций и интеграла Лебега сохраняются с соответствующими видоизменениями и в абстрактной теории меры и интеграла. Последняя составляет математическое основание современной теории вероятностей, данное в 1933 А. Н. Колмогоровым. Специальный интерес для ряда областей математики представляют меры, инвариантные по отношению к той или иной группе преобразований множества U в себя.
Лит.: Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Лебег А., Интегрирование и отыскание примитивных функций, пер. с франц., М. - Л., 1934; Сакс С., Теория интеграла, пер. с англ., М., 1949; Халмош П. Р., Теория меры, пер. с англ., М., 1953.
Ю. В. Прохоров.
Меры теория
АДДИТИВНАЯ ЧИСЛЕННОЗНАЧНАЯ ФУНКЦИЯ ОТ МНОЖЕСТВА
Носитель меры; Пространство с мерой; Конечно-аддитивная мера; Σ-аддитивность; Теория меры; Счётно-аддитивная мера; Мера (математика); Финитная мера; Меры теория
раздел математики, изучающий свойства мер множеств (см. Мера множества). М. т. возникла на основе работ М. Э. К. Жордана, Э. Бореля (См. Борель) и в особенности А. Лебега в конце 19 - начале 20 вв., в которых понятия длины, площади и объёма распространялись за пределы класса обычно рассматриваемых в геометрии фигур. Впоследствии предметом М. т. стали меры в наиболее общем понимании (вполне аддитивные функции множеств). Развитие М. т. тесно связано с развитием теории Интеграла.
Мера множества
АДДИТИВНАЯ ЧИСЛЕННОЗНАЧНАЯ ФУНКЦИЯ ОТ МНОЖЕСТВА
Носитель меры; Пространство с мерой; Конечно-аддитивная мера; Σ-аддитивность; Теория меры; Счётно-аддитивная мера; Мера (математика); Финитная мера; Меры теория
Ме́ра мно́жества — числовая характеристика множества, интуитивно её можно понимать как массу множества при некотором распределении массы по пространству. Понятие меры множества возникло в теории функций вещественной переменной при развитии понятия интеграла.
Мэра (дочь Прета)
ПЕРСОНАЖ ДРЕВНЕГРЕЧЕСКОЙ МИФОЛОГИИ
Мера (дочь Прета); Майра (дочь Прета)
Мэра (Майра, ) — персонаж древнегреческой мифологии. По одной родословной, дочь Прета (внука Сисифа).
Мера Хаусдорфа
МЕРА МНОЖЕСТВА
Линейная мера; Плоская мера; Цилиндрическая мера; Альфа-мера Хаусдорфа; Хаусдорфова мера
Мера Хаусдорфа — собирательное название класса мер, определённых на борелевской \sigma-алгебре \mathcal{B}(X) метрического пространства X.

